Raspberry Shake Basic Concepts

March 27th, 2025 – by Alan Sheehan and Philip Peake

So, you’ve bought yourself a Raspberry Shake… now what? Once you have set up and connected your device, one of the first things you’ll want to do is to have a look at the data it produces. There are a number of ways to do that, but one of the simplest and most versatile ways is to use the Raspberry Shake Data View web app.

In this blog, we’ll discuss some basic background information about Raspberry Shakes and earthquakes to help you understand what you can see on DataView.

There are multiple different programs and presentation styles for the data gathered from sensors measuring earth movement. In this document, we will concentrate on the Raspberry Shake DataView application, which is a web-based software that archives the data from all Raspberry Shakes and displays it in (very close to) real-time. This can be accessed here.

This will display a list of online Raspberry Shakes and a blank display panel. Expand one of the ‘Shakes in the list, and you will see a list of its different sensors. Most Raspberry Shakes have only one (EHZ), which measures movement in the ‘Z’ axis (up and down). There are also Raspberry Shakes which have sensors measuring along three axes (X, Y and Z) with the X and Y axes aligned North-South and East-West. There may also be an HDF sensor, which measures very low-frequency air pressure changes (infrasound).

Typically, you might access Data View by providing the name of your Raspberry Shake and the sensor you want to view.

Example of my ‘Shake:

Name: R309F  |  Sensor: EHZ

If you haven’t done so yet, it is well worth your time to click on the red question mark at the top right of Data View to take a tour of the software.

By default, you see a “plot” covering the last 24 hours (Fig. 1). This is referred to as a “helicorder plot.” It mimics the old-style seismographs with a pen recorder writing on paper wrapped around a drum which slowly turned and moved horizontally to trace a spiral around the drum.

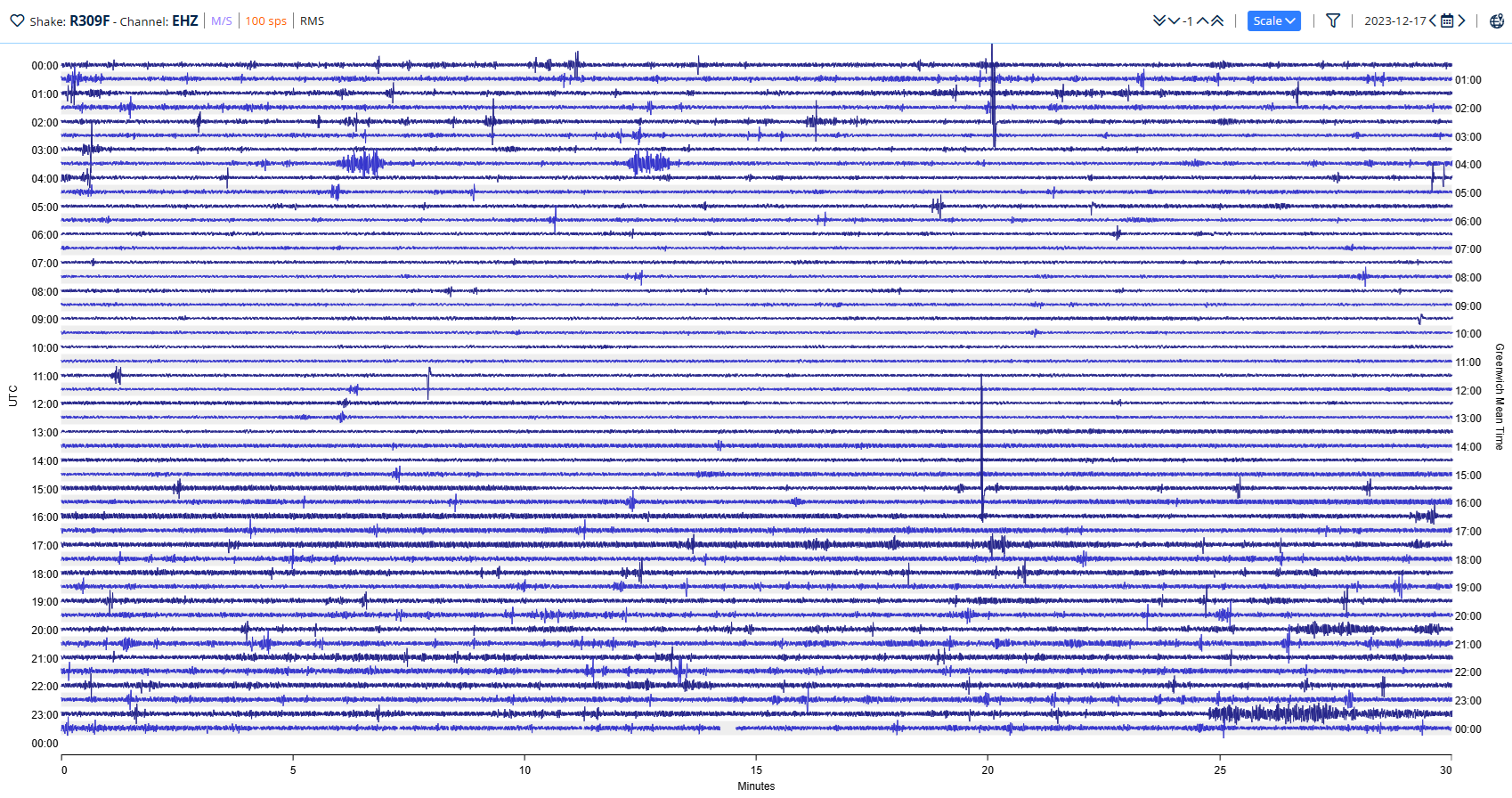
Figure 1: DataView Helicorder plot

What can you see on the helicorder? The station name and channel can be found at the top left of the window, and beside the channel, you will see the units of the measurements on the helicorder. In this case, m/s tells you the trace on the helicorder shows the velocity of the vibrations in meters per second. Geophone sensors, such as those used in the EHZ channel, measure velocity. The old mechanical drum-type seismographs measured displacement (i.e., how far the ground moves), while geophones measure how fast it moves. The other sensor used in Raspberry Shakes is the accelerometer, which, as the name suggests, measures the acceleration of the ground in m/s² (meters per second squared).

As the helicorder shows 24 hours of data at a time, interesting events can be identified for further investigation. This is done by clicking on the helicorder plot at the point you are interested in, and a close-up view of the waveform in that area will pop up. For example, notice the strong signal in the lower right corner of the helicorder. It is the start of a signal from a distant earthquake, and close up, it looks like this:

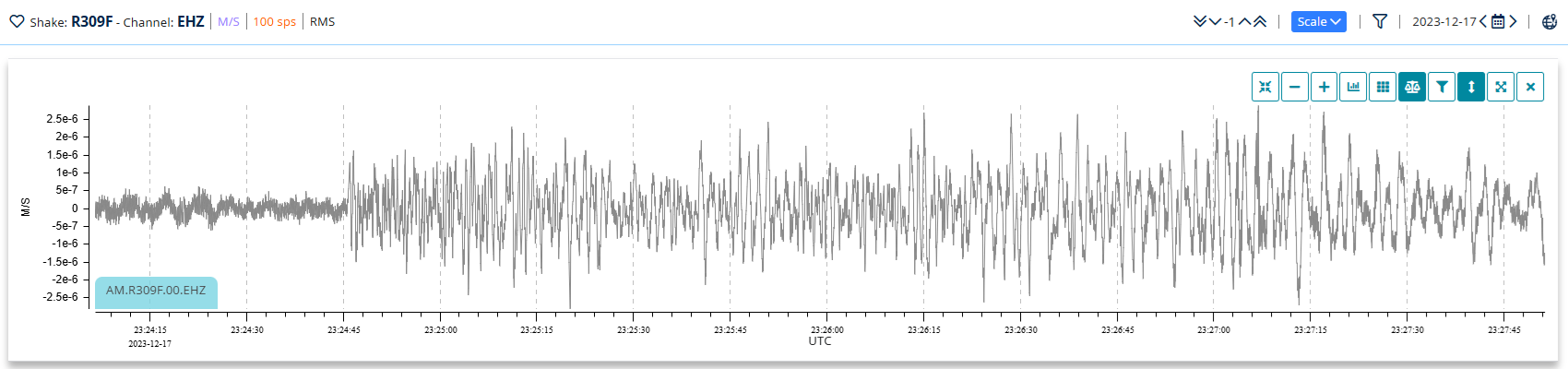
Figure 2: DataView detail plot

The naming convention for Raspberry Shakes is:

• EH = a geophone channel
• SH = a geophone channel
• EN = an accelerometer channel.
• Z = Vertical (Up-Down) channel (up is the positive direction)
• E = Horizontal East-West channel (East is the positive direction)
• N = Horizontal North-South channel (North is the positive direction)

So, the EHZ channel in the example above is a vertical geophone channel. All Raspberry Shakes (except for a Raspberry Boom) have an EHZ or SHZ vertical geophone channel.

The other channel you’ll come across in Raspberry Booms and Raspberry Shake and Booms is the HDF channel.

HDF = infrasound channel (increased air pressure is positive) measured in Pa.

Infrasound is technically sound below the minimum audible frequency of human hearing (i.e., <20 Hz), but the Raspberry Boom HDF channel can detect up to 50 Hz. It is useful to be able to process and present the infrasound signals in the same way as seismic signals, especially as, in some cases, there is a connection.

The signals the Raspberry Shake measures are made up of many different frequencies.

The design of the Raspberry Shake allows it to collect data at 100 samples per second (sps), which in turn means the maximum frequency the Raspberry Shake can detect is 50 Hz. So what you see in the signal from your Raspberry Shake is a lot of different frequencies up to 50 Hz, all mixed: some strong, some weak, some growing, some decaying, some may be entirely missing. The frequencies and their timing, strength, attack (growth), decay, or absence can be interpreted to determine the source or cause of the signal (or noise).

Along with the signals we’re interested in, there will also be a lot of “noise”. By noise, we simply mean unwanted signals or interference. Noise could be caused by signals from other events that we are not interested in; it may be true noise, such as radio interference, noise due to thermal effects in the sensors, the Raspberry Pi computer itself, etc. But noise is basically signals we aren’t interested in at the time.

The most powerful tool we have to deal with noise are filters. Filters can be defined as: 

• Low Pass (allow all frequencies below a specified frequency through).
• High Pass (allow all frequencies above a specified frequency through). Or
• Band Pass (allow only frequencies between two specified frequencies through). 

Data View allows filters to be applied to both the helicorder and the detailed waveform view, if desired. We will talk more about filters later on.

So, how do we identify what frequencies make up the signal? This is where Fast Fourier Transforms (FFT), Power Spectral Density (PSD), and Spectrograms come in…

A signal received on a Raspberry Shake is made up of many frequencies, just like noise and music are. A Fast Fourier Transform is a mathematical algorithm that works out what frequency pure sine and cosine waves make up the signal and how strong (how much amplitude) each frequency has. This is a powerful tool because, once we know the frequency of a vibration, we might be able to identify its source.

You may come across the terms “Time domain” and “Frequency Domain”, particularly in relation to FFTs. In simple terms, the original signal plotted against time (on the x-axis of the graph) is “in the time domain”. When an FFT is applied to a signal, the result is plotted against frequency (on the x-axis of the graph), which is said to be “in the frequency domain”.

A FFT can always be recreated from the original signal, but the original signal can’t be recreated from the FFT. This is because the FFT algorithm ignores and loses information about phase, timing, attack, and decay.

Power Spectral Density (PSD) plots get their name from electrical signal processing, because the electrical signal (either volts or amperes) is converted to Power (W) before plotting.

The electrical formulae P = I²R and P = V²/R (where P = power in Watts, V = voltage in Volts, I = current in Amperes, R = resistance or impedance in Ohms) are used to calculate the Power. Hence, the basis of the PSD is that the FFT of the signal is squared, multiplied/divided by any relevant factors, and then multiplied by the resolution of the frequency axis (bin width).

As the FFT of the signal is squared in a PSD plot, the variation in “Power” between different frequencies is often significant, so PSDs are usually plotted or calculated on logarithmic scales. 

PSD plots are often used to analyze signals that are made up of predominantly random frequencies (such as earthquake signals). In contrast, FFT plots tend to be preferred for less random signals, such as those obtained from machines during vibration analysis or when searching for specific frequencies, i.e., fault frequencies in vibration analysis.

As a result, Data View uses Power Spectral Density (PSD) plots to display frequencies from a close-up waveform view (Fig. 3).

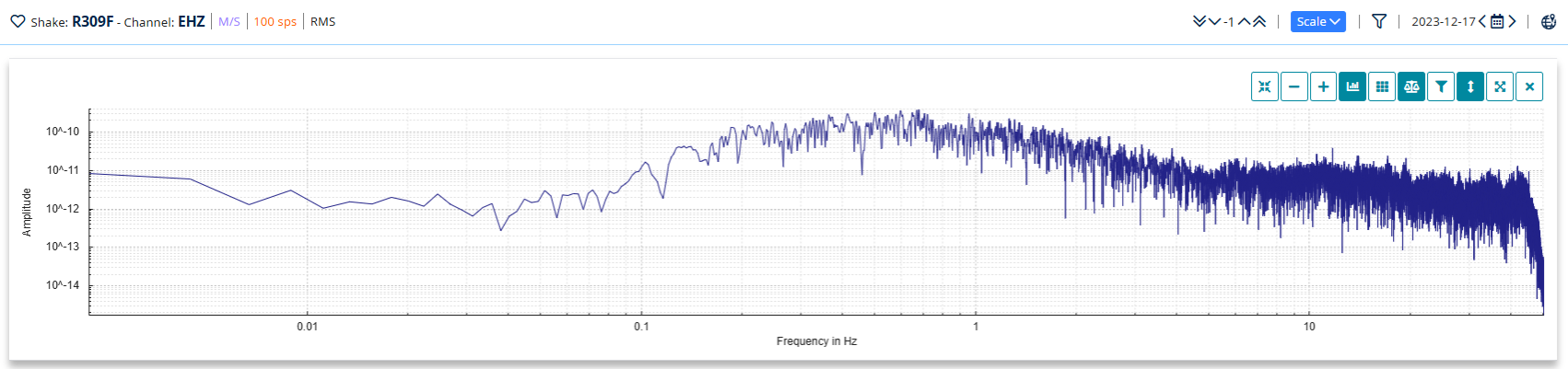
Figure 3: Power Spectral Density (PSD) plot

Note that the actual magnitude of the PSD plot is affected by the plot’s resolution (bin width), so while PSD plots produced by different methods or parameters may show a similar shape, the numerical values are likely to be different. This can be a trap when comparing PSDs for two different time periods – they must be the same length sample (and so the same bin width) for a valid comparison.

Note also that comparing a PSD from Data View with, for example, a PSD from Matplotlib or another source is likely to result in numerical discrepancies, even though the plot may show the same/similar shape.

The spectrogram is a really powerful visualization of Frequency v Time. Frequency is plotted on the Y axis, and Time along the X axis. Apart from frequency information, it also shows some timing information.

The signal strength for each frequency is displayed in color using an appropriate color map. Typically, weak frequencies will be plotted in dark tones, while strong frequencies will appear brighter (depending on the color map used). By default, Data View uses a color map called Inferno, which starts at black and increases through purples, reds, oranges, and yellows at the high end of the color map. So, yellows represent strong frequencies, and black and dark purples represent weak frequencies.

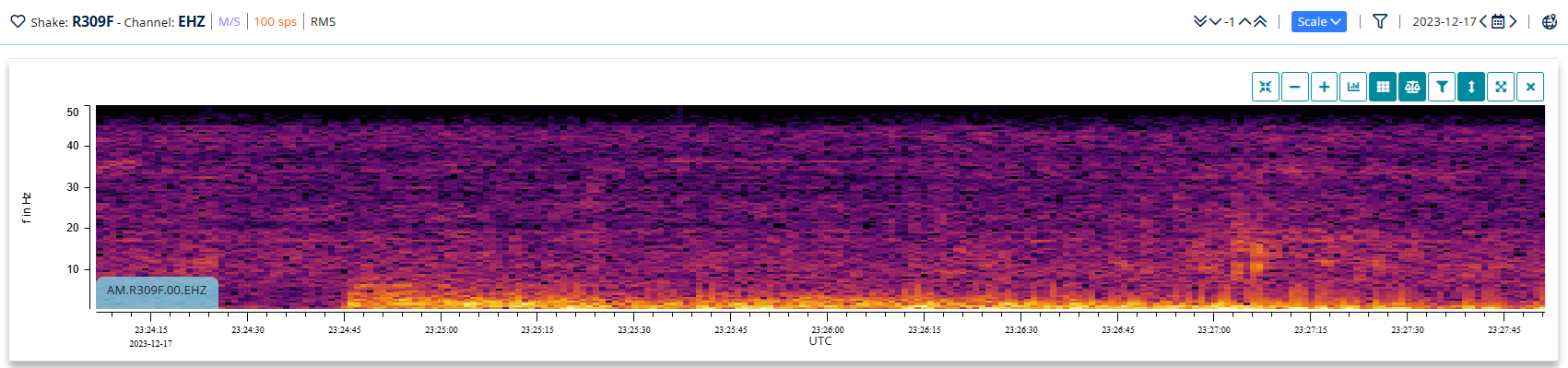
Figure 4: DataView spectrogram plot

The spectrogram (Fig. 4) of the same earthquake in Fig. 1 and Fig. 2 is made by calculating an FFT for each time interval and plotting the results in the vertical column with the signal strength colourized. This way, it shows when signal frequencies start and stop, grow (attack) and decay, and even change in frequency as the source slows down or speeds up.

The most common cause of earthquakes is the movement of tectonic plates. As the plates of the Earth’s crust move past each other, they can interlock and they can also stick to one another due to friction. As the plates continue to move but the edges stay in contact, stress builds up until the edges move past each other suddenly, releasing the stress and resulting in an earthquake.

Other tectonic effects away from the plate edges include the buckling of rocks due to excessive stress, which may result in the formation of mountains, folds, and rifts. Whenever rock is broken or slips along fault lines due to excessive stress, these events also produce earthquakes.

Other sources of earthquakes include volcanism (eruptions, and development of magma chambers), explosions, and other mechanisms that can distort and/or fracture rock. The largest earthquakes from these sources are usually not as large as those from tectonic sources.

Earthquakes produce two main types of vibration, which propagate through and around the world as waves: P waves and S waves. There are others, such as surface waves, but we are not concerned with them here. P waves are compression waves (similar to sound waves in air) that travel through the Earth. S waves are shear waves as a result of the shearing of rock in the earthquake.

P waves are longitudinal waves, so the back-and-forth movement of particles due to the P wave is in the direction of motion of the wave.

S waves are transverse waves, so the movement of particles due to the S wave is perpendicular to the direction of motion of the wave.

P waves travel through rock faster than S waves, so typically, P waves arrive before S waves. (The terms P and S originally referred to Primary and Secondary waves reflecting this difference in speed).

As pressure and temperature increase with depth in the Earth, the wave speeds increase with depth as well. This means the fastest way between the earthquake and the Raspberry Shake is not a straight line as might first be expected but is, in fact, a curved path downwards from the earthquake and upwards towards the station.

The waves from a close earthquake do not go very deep before returning to the surface, so the approach angle of the wave is relatively shallow. This can be seen in the following plot (Fig. 5) of earthquake ray paths:

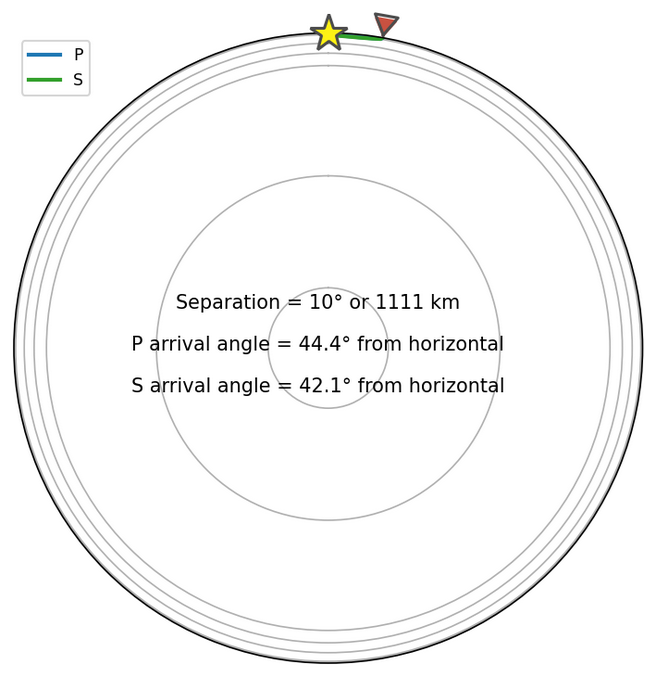
Figure 5: Local earthquake P and S waves ray paths

This is a model of an earthquake 10 km deep (the star) and the Raspberry Shake Station distant 10° on the Earth’s surface. 

As you can see, the ray paths are quite shallow. In this case, the P waves (which push back and forth) push slightly more in the horizontal direction than vertically (but they are nearly equal). The S wave, however, is a transverse wave, so while the S wave arrives ever so slightly flatter, the particle motion from the wave is more in the vertical direction than the horizontal.The ray paths for a more distant earthquake are more like this (Fig. 6):

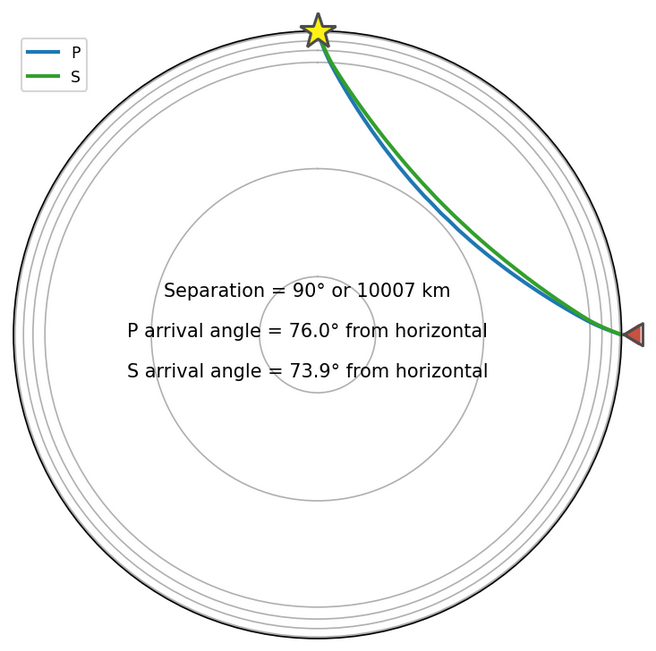
Figure 6: Distant earthquake P and S waves ray paths

In the case of a distant earthquake, the P wave (being a longitudinal wave) delivers most of the energy in the vertical direction, being weak horizontally, and the S wave (a transverse wave) puts most of its energy and movement into the horizontal direction and appears weak in the vertical direction. There will also be a longer time period between the P wave and the arrival of the S wave.

Here is an example of a close earthquake on the EHZ channel of a Raspberry Shake (Fig. 7 – Note: the P/S wave markers in this and any other similar figures have been added for illustration purposes only):

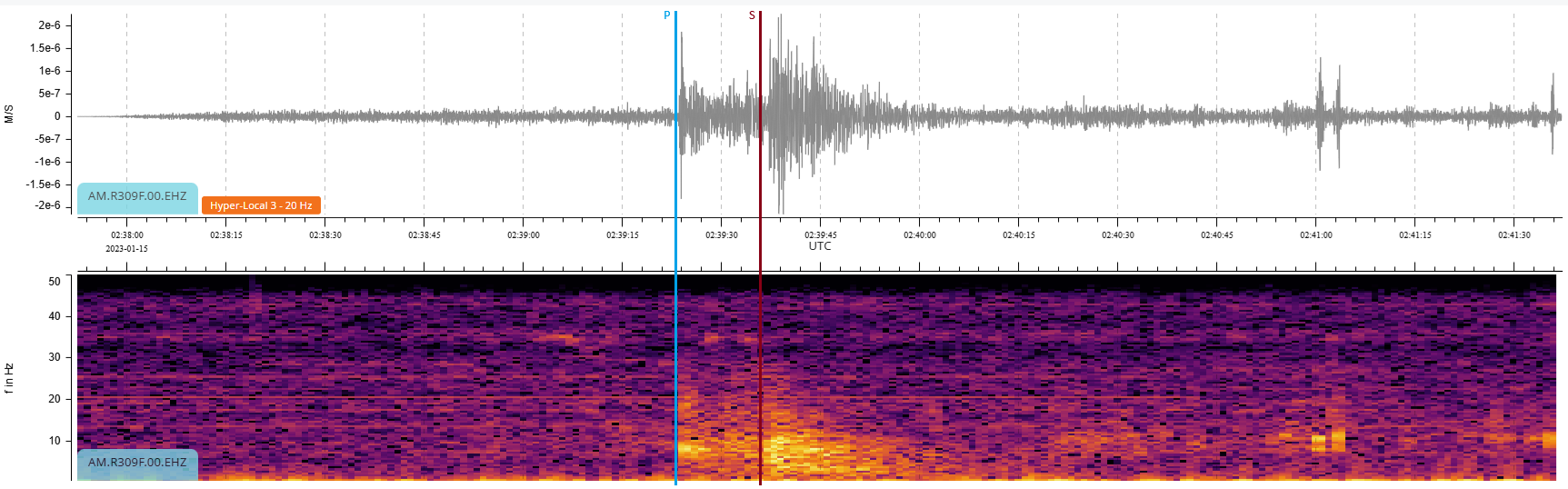
Figure 7: Local earthquake P and S arrivals

The P wave can be seen to arrive at 02:39:23 UTC, and the S wave arrives at 02:39:36 UTC (each tick mark is 3 seconds). We know the earthquake is close because there is not much time between the P and S waves.

We can also see that the S wave is larger in amplitude than the P wave. The sensor is the EHZ channel, measuring the vertical movement of the ground only, so as the approach angle is shallow, the vertical component of the P wave is relatively small, and the vertical component of the S wave is quite high. (In this case, an EHE or EHN horizontal channel would probably show a slightly stronger P wave and a weaker S wave).

For a more distant earthquake, the P wave would show higher amplitude (as the approach angle is steep), and the S wave would be a long time behind the P wave and relatively weak in the EHZ channel as the vertical component of the S wave would be very small. (In this case, an EHE or EHN channel would probably show a weaker P wave and a much stronger S wave).

Sudden events such as spikes, and step signals like earthquakes, release ALL frequencies from very low to very high. We know this from the mathematical Fourier Series for a step change or a spike. High frequencies are attenuated (reduced in amplitude over distance) more quickly than low frequencies, so it is evident in the above spectrogram that both P and S waves fade out at about 25 Hz. Generally, it is more likely to see higher frequencies in close earthquakes than in distant ones. Often, distant earthquakes will fade out in the spectrogram at about 2 or 3 Hz. This is, of course, affected by both the distance and the magnitude of the earthquake, so larger quakes will produce stronger signals that take further to attenuate.

For this reason, very low frequencies (below 2 or 3 Hz, for example) are very important in identifying and monitoring earthquakes.

Here is another example of a close earthquake: an M3.9 just 83 km away (Fig. 8).

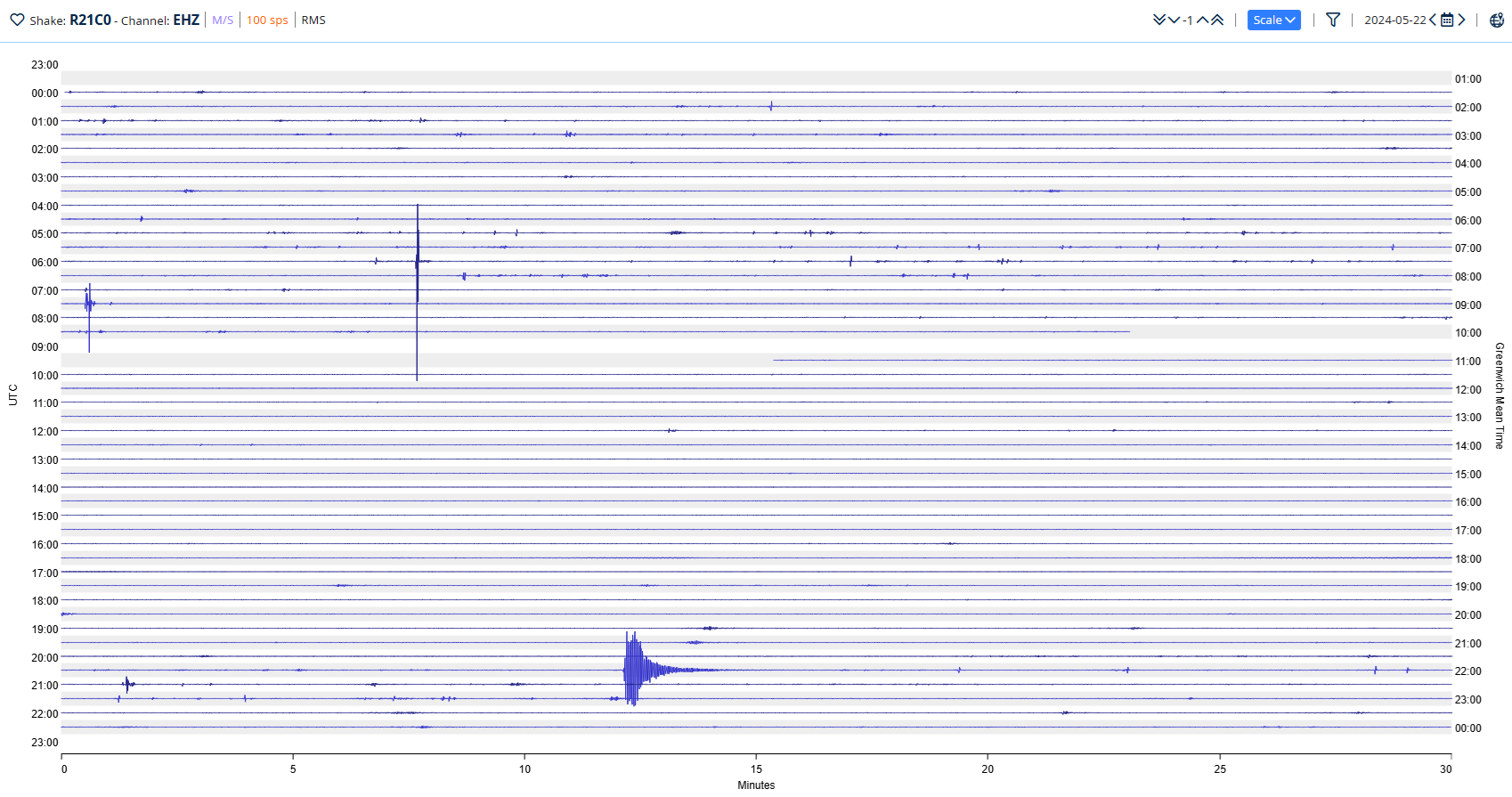
Figure 8: Local earthquake helicorder view

That’s it at around 20:42 UTC on the helicorder. In detail (Fig. 9), it looks like this (note that stations R21C0 and R4FA0 are at the same location):

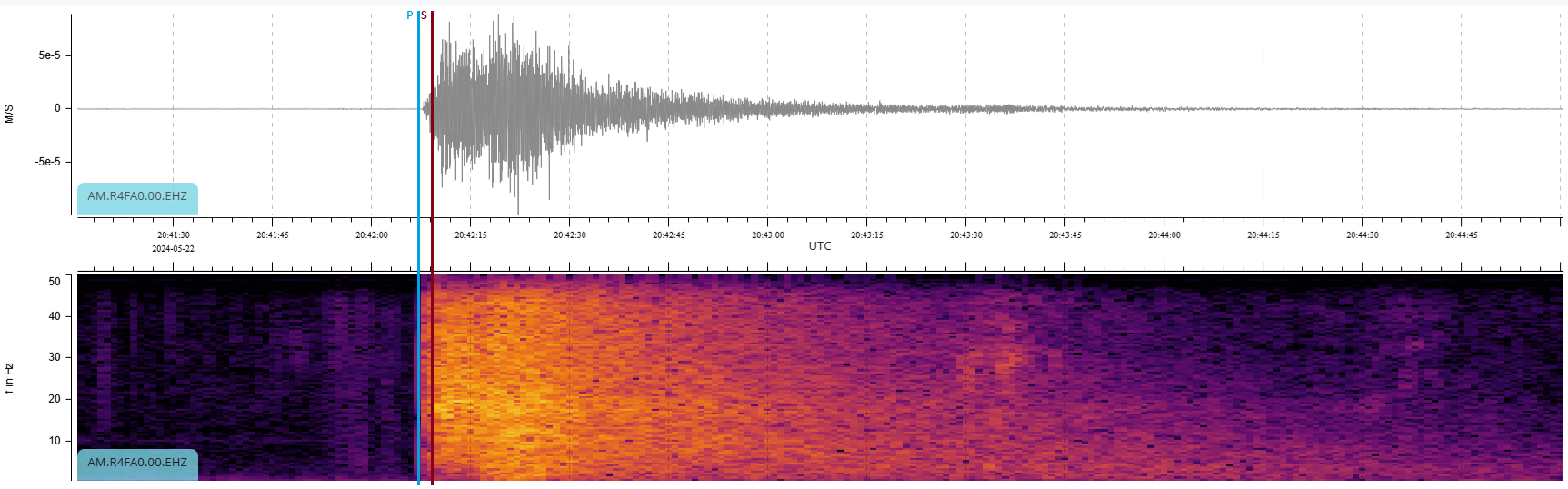
Figure 9: Local earthquake detail view

The P wave arrival time is 20:42:08 UTC, and the S wave arrival time is 20:42:11 UTC (each tick mark is 3 seconds).

Notice the P and S arrivals are not so distinct in the waveform with very close earthquakes. Also notice the “trumpet-shaped” decay in the waveform after the S wave.

Looking at the spectrogram, notice that the earthquake produces the full range of frequencies but that the higher frequencies decay faster. They also attenuate faster with distance, so they don’t appear on distant seismometers. This produces the typical triangular decay shape on the spectrogram typical of an earthquake regardless of distance.

One finer detail to notice on the spectrogram is the weakness in very low frequencies from the P wave. The following S wave fills in these frequencies when it arrives. This may or may not always be evident, depending on the characteristics of the quake, but it helps to confirm the arrival of the S wave when it is apparent.

In the horizontal channels of a 3D Shake, this same quake appears as follows (Fig. 10 and Fig. 11):

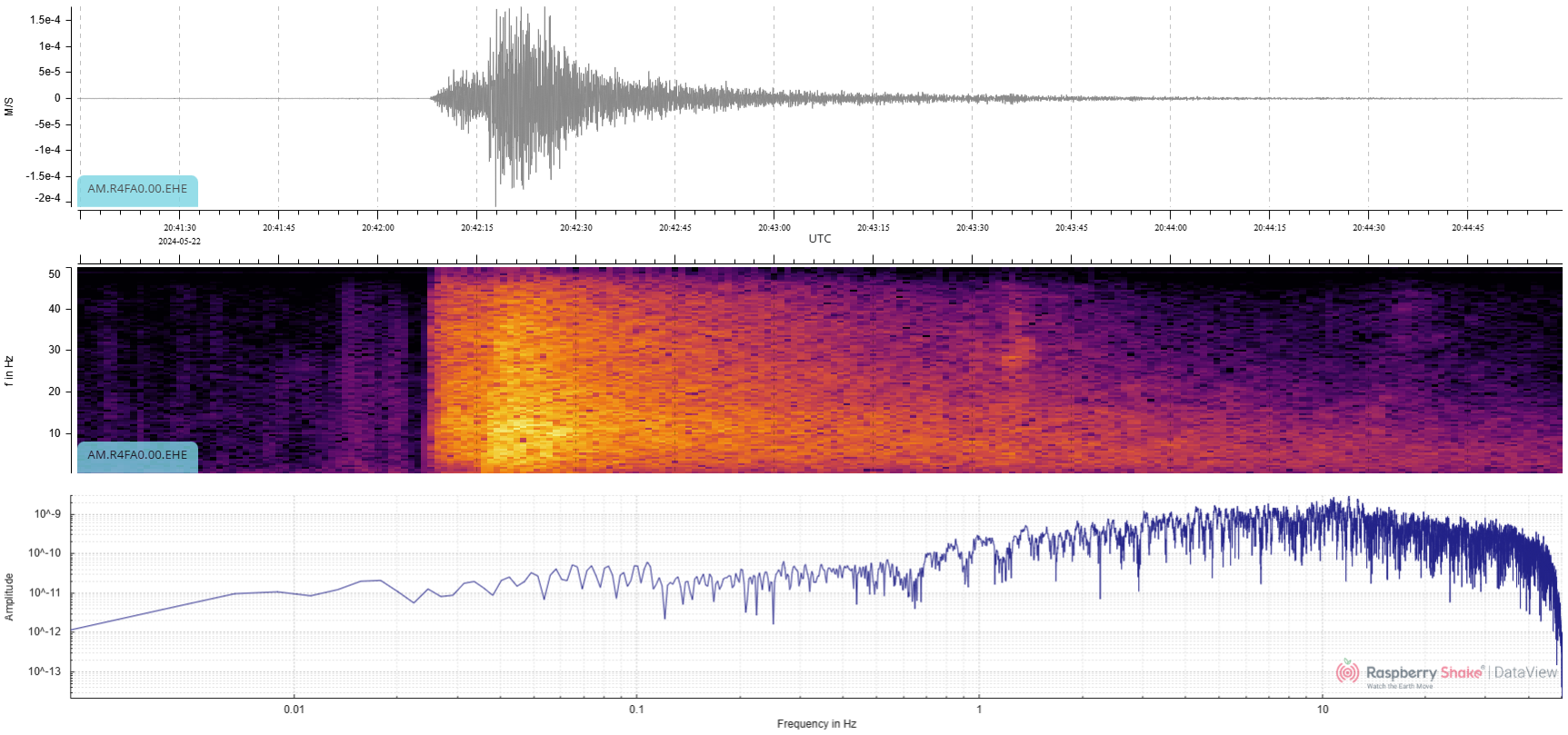
Figure 10: Local earthquake detail view – EHE channel

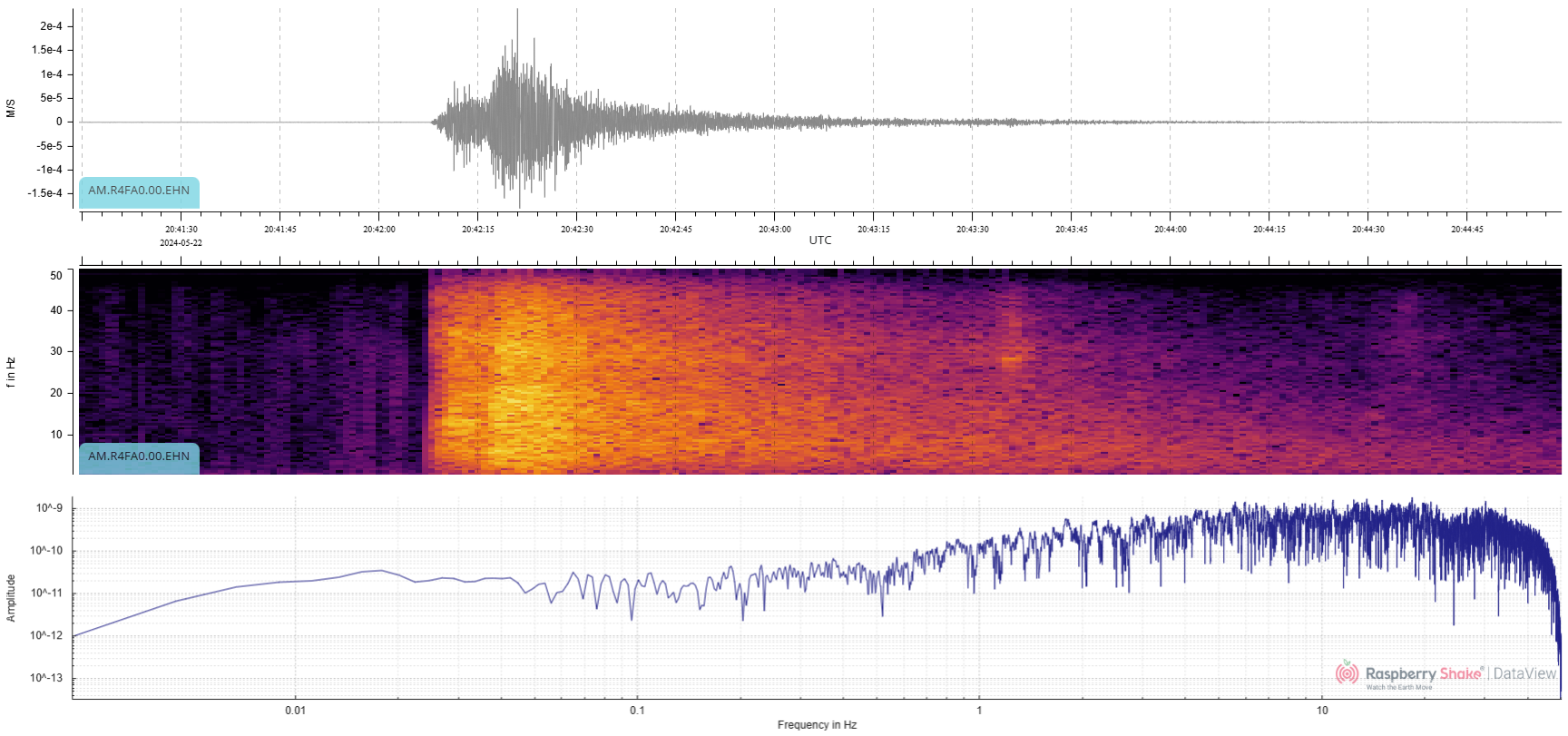
Figure 11: Local earthquake detail view – EHN channel

Notice that the P and S arrivals are more distinct in waveforms and spectrograms.

Also, notice that the amplitude of the horizontal waves in the EHE and EHN channels is about 2.5 times that of the vertical waves in the EHZ channel. This results from the close earthquake and the waves approaching at a shallow angle (this earthquake was at a depth of just 1 km and 83 km away).

In the PSD curves for all three channels (EHZ, EHN, and EHE), the peak power in the PSD curves is in the range of 10 to 20 Hz. The peak power for more distant seismometers will be at lower frequencies as the higher frequencies attenuate with distance. The further away from the earthquake, the lower the peak power in the PSD curve will be.

As mentioned earlier, Filters are one of the most powerful tools we have at our disposal for visualizing the source of signals and separating them from noise. By selecting the appropriate filter, most unwanted noise can often be removed to reveal the signal of interest.

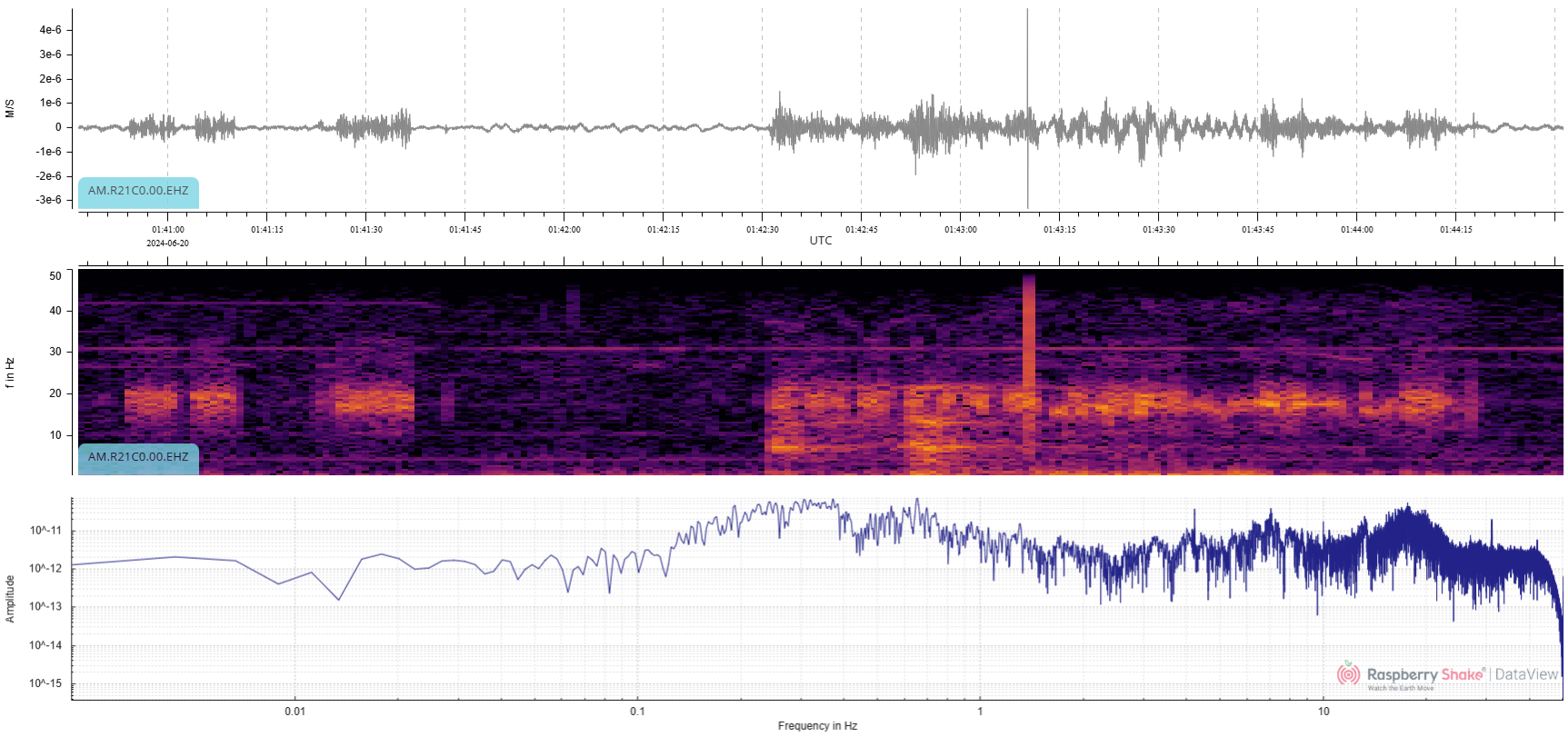
Figure 12: Unclear raw waveform detail view

In this example (Fig. 12), the waveform is not clear; there may be a signal there that’s of interest, or maybe it’s all just noise, but when we inspect the spectrogram, it looks like there could be a small earthquake signal (or in fact, in this case, a mine blast) arriving at 01:42:32 UTC.

If we apply a bandpass filter, we can reject all the noise we don’t want and reveal the signal that we do.

Filters are applied using the filter button on the waveform pop-up (Fig. 13):

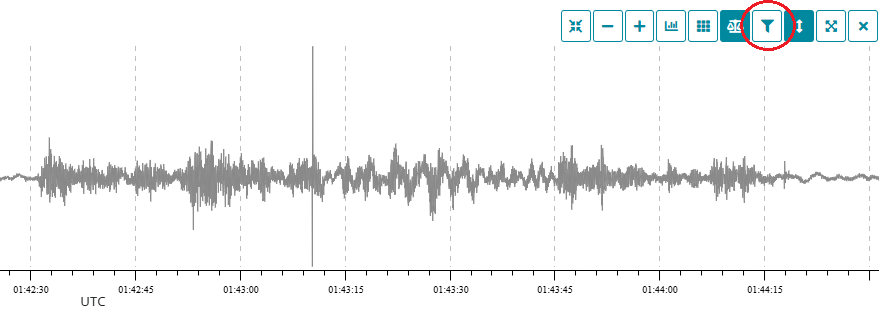
Figure 13: Filter button in Data View detail panel

When you click the filter button, another pop-up will allow you to enter the lower and upper frequencies of the bandpass filter. To use a low pass filter, enter the upper frequency only, and likewise, to use a high pass filter, only enter the lower frequency. To remove the filter and return to full bandwidth, enter -1 in both lower and upper frequencies.

Applying a 0.7 to 10 Hz bandpass filter results in the following output (Fig. 14):

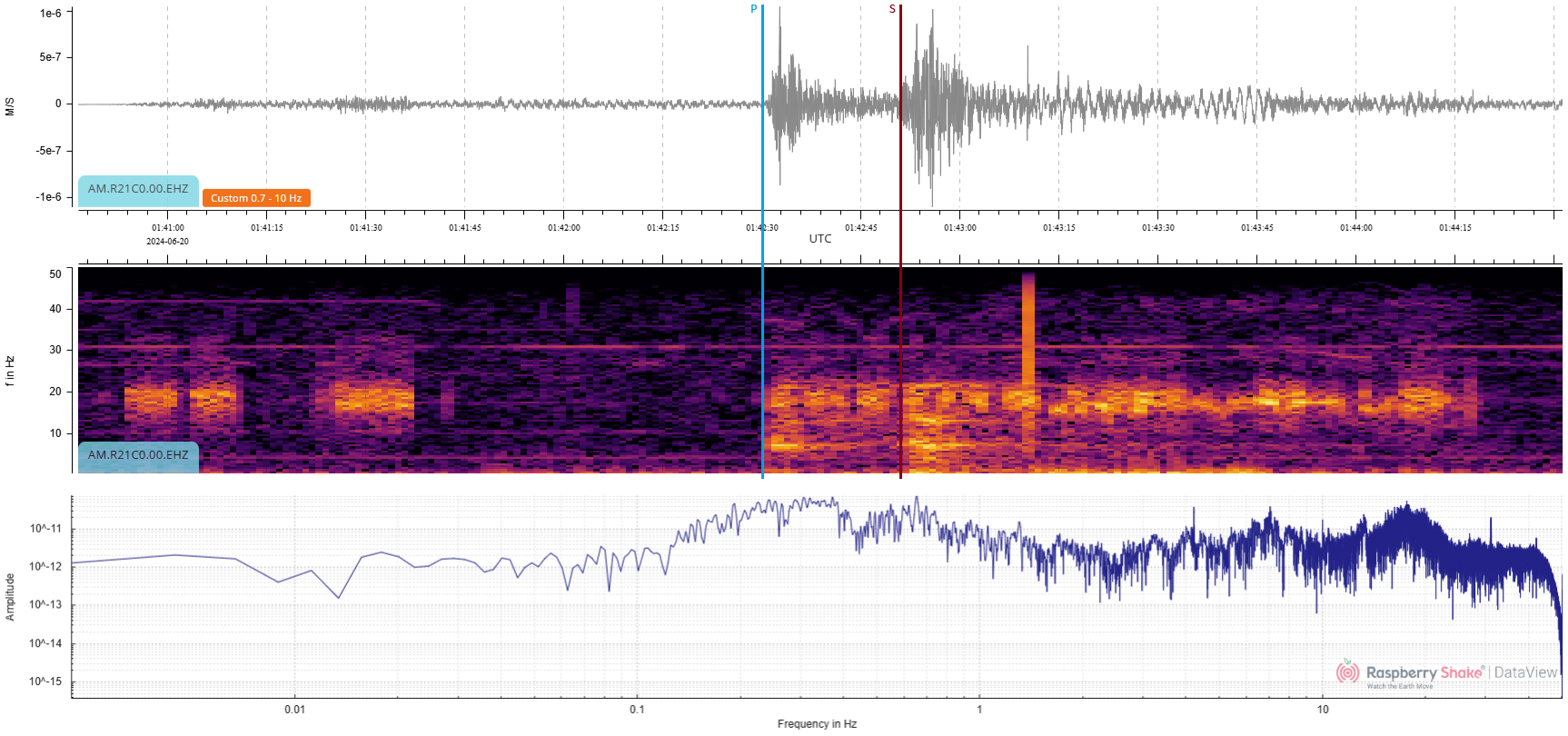
Figure 14: Unclear waveform – now filtered

Notice the waveform is much cleaner and shows the typical characteristics of a small close earthquake (the only clue that is, in fact, a mine blast is in the spectrogram where a strong horizontal line at 7 Hz indicates a detonation interval of 1/7 s or 0.143s – earthquakes will not show such a line). The frequency of the line can be checked accurately on the spectrum/PSD, where it shows as a peak.

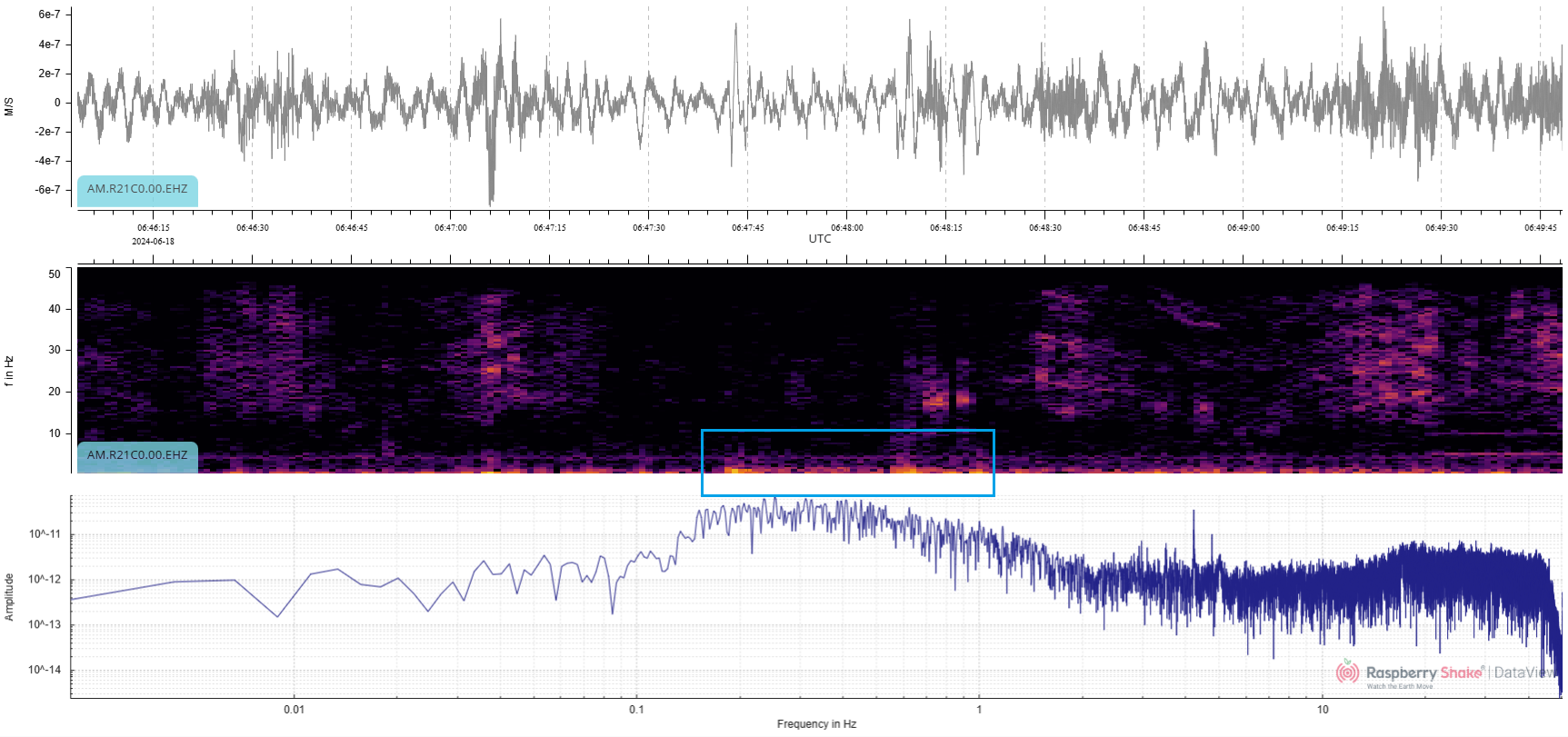
Figure 15: Another unclear waveform detail… or not?

Looking at the waveform in this example (Fig. 15), it is difficult to say whether there’s an interesting signal. It may just all be noise. But look closely at the spectrogram at 06:47:42 UTC, and a small bright color spike is visible right at the bottom. This small area of brighter tones turns out to be the P wave arrival of an M5.8 earthquake in Tonga, 4087 km away.

We can clean up the waveform by applying a 0.7 to 2 Hz bandpass filter (typical choice for distant quakes), and it looks like this (Fig. 16):

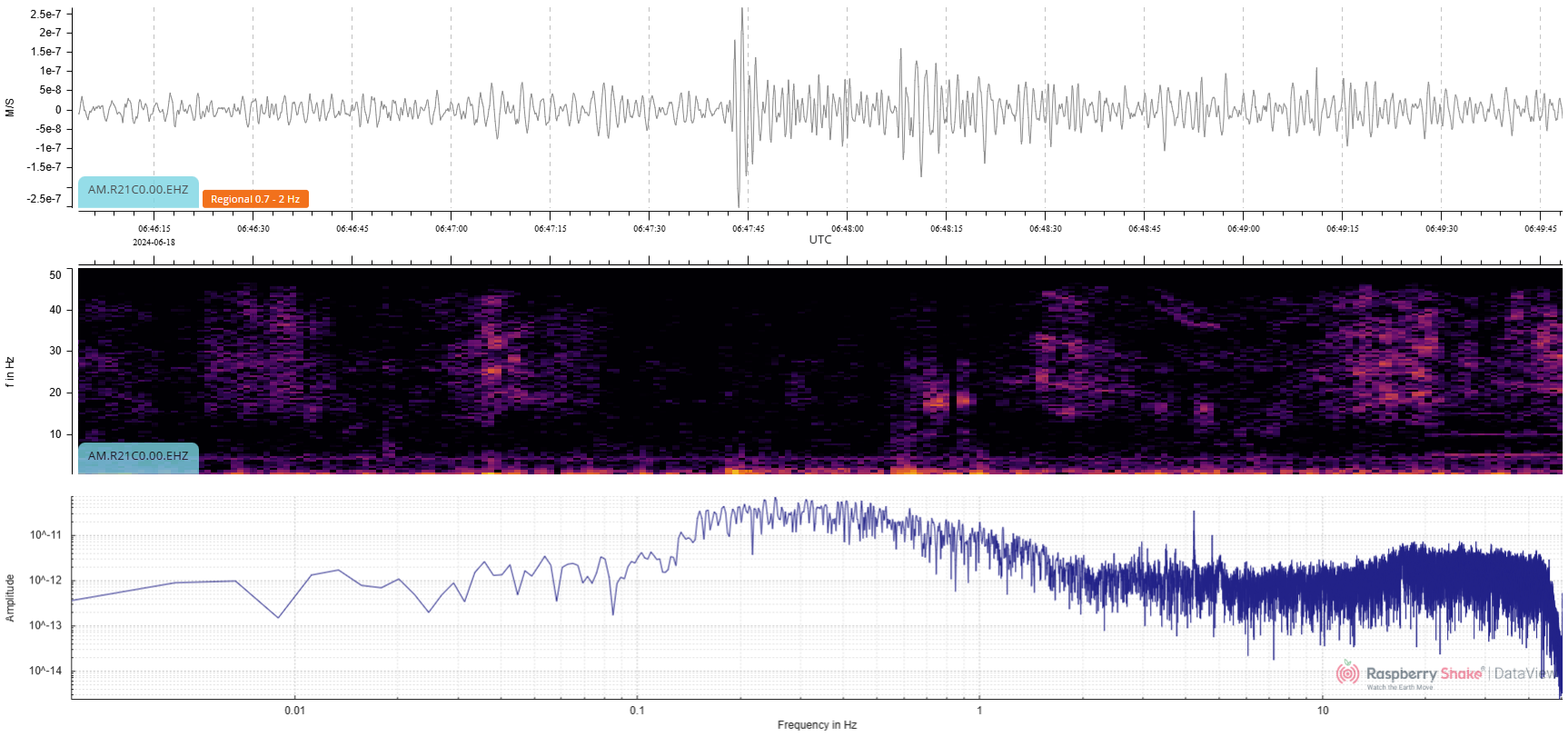
Figure 16: The P wave is now very clear after the application of filters

Notice that the filters are not applied to the spectrogram or the spectrum/PSD plot.

Maybe your Raspberry Shake installation isn’t ideal… actually, it’s likely that, in lots of cases, it won’t be. That’s OK. Below is a helicorder with plenty of “Cultural Noise” (Fig. 17).

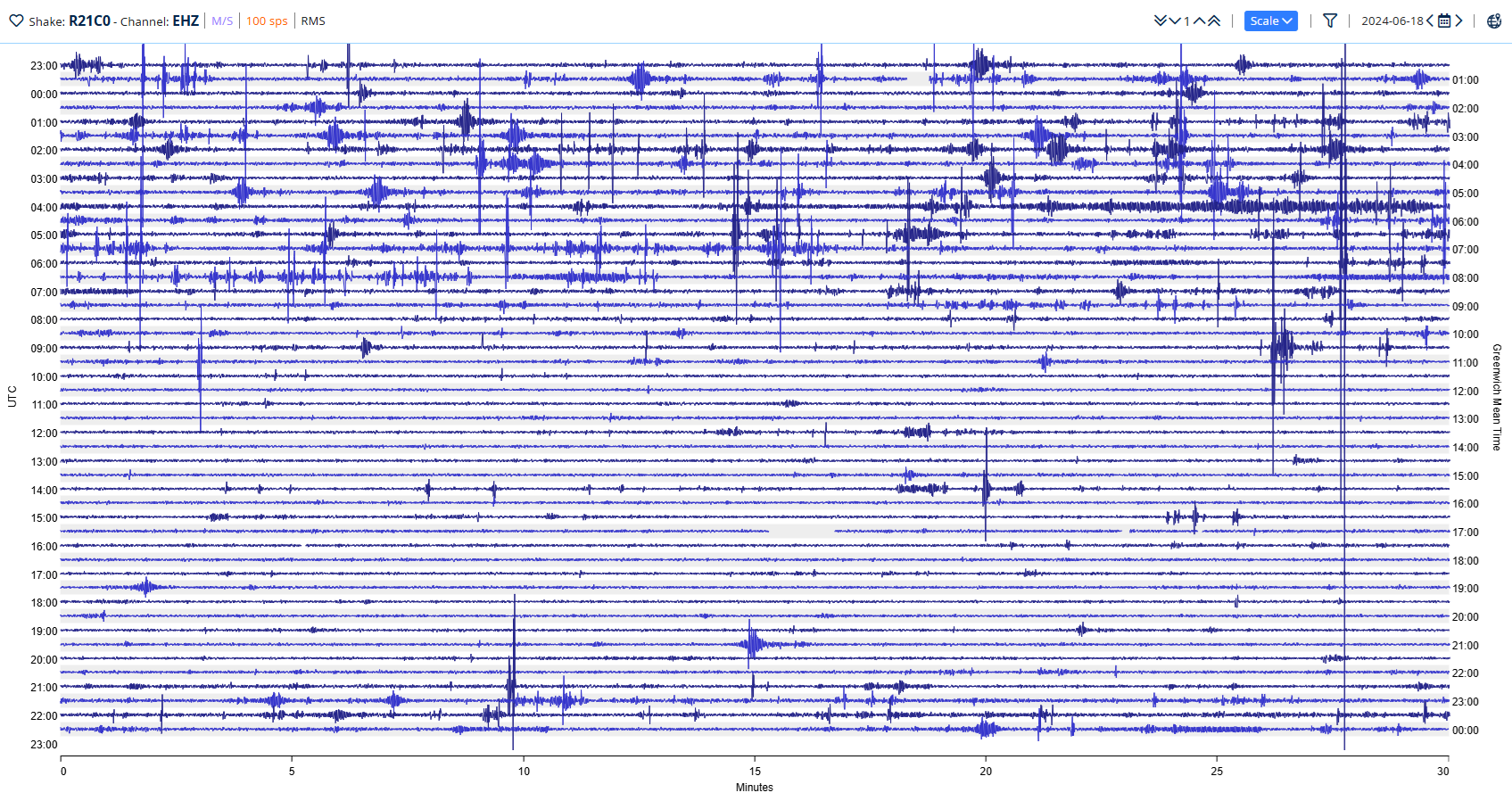
Figure 17: DataView helicorder view with much cultural noise

Many of the spikes and higher color density areas on this helicorder are known to be passing log trucks, which are also known to be weak in frequencies below 10 Hz, so we could apply a low pass filter to the helicorder to remove them and allow us to see only what’s detected in the 0 to 10 Hz range.

In the top right-hand corner of the helicorder plot, you’ll find a filter button (it should be familiar to you after the last section) between the Scale button and the Date. This brings up a pop-up to allow the filter frequencies to be applied to the helicorder just as we did before to the waveform.

Figure 18: Helicorder filter pop up

This is what the filter pop-up looks like for a 10 Hz low pass filter (Fig. 18).

And this is what the helicorder looks like after it is applied (Fig. 19):

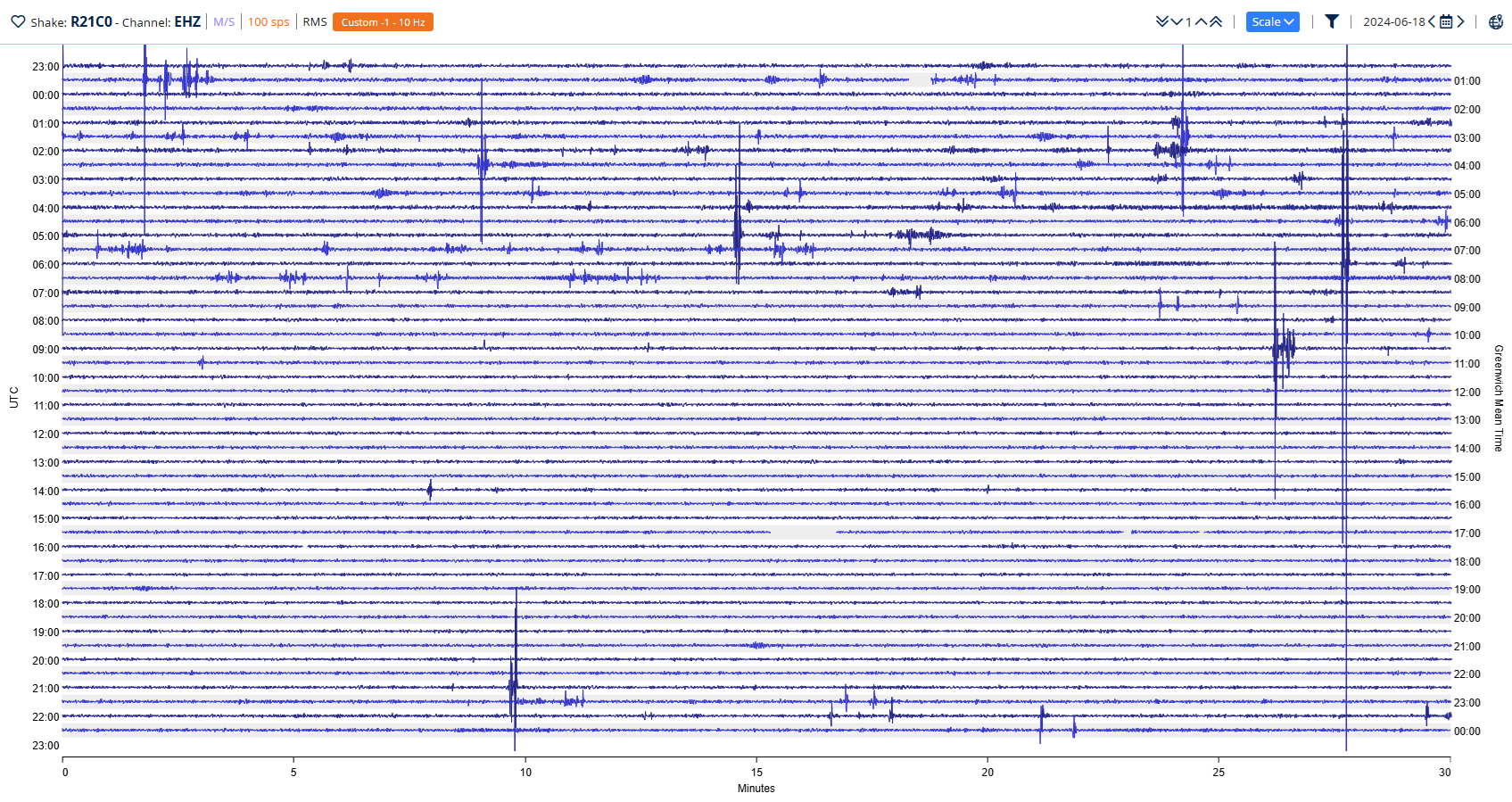
Figure 19: 10Hz low pass filtered Helicorder display

As you can see, the spikes from the passing truck are significantly reduced, but nothing particularly interesting has emerged, so let’s try applying a 0.7 to 2 Hz bandpass filter (Fig. 20):

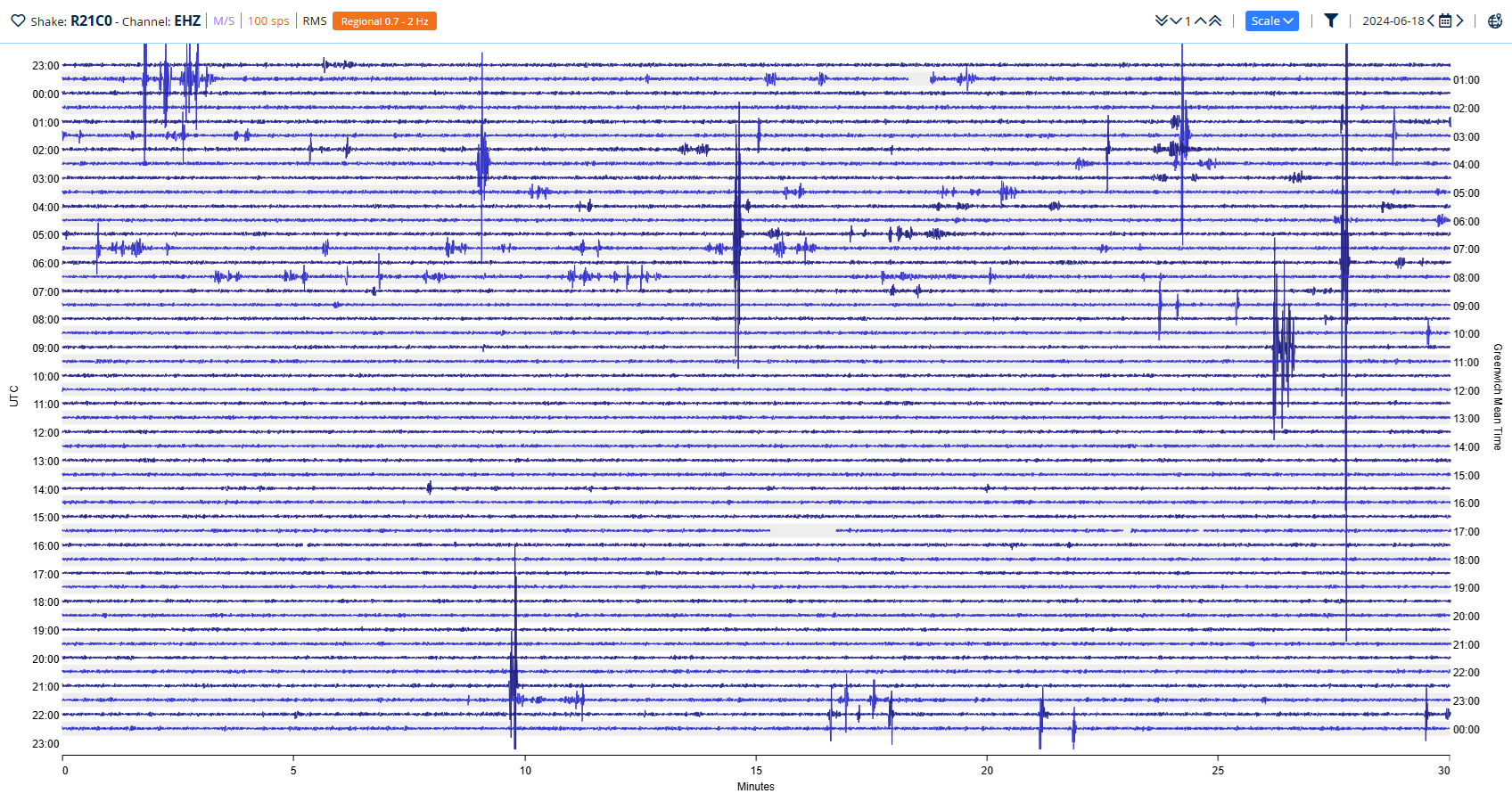
Figure 20: 0.7 to 2.0Hz bandpass filtered Helicorder display

Now, if you look at 06:47:30 UTC, the signal from the M5.8 earthquake in Tonga (from the previous example in Filtering the Waveform) should just be visible.

Note that filters applied to the helicorder are not transferred to the waveform plot. The helicorder and waveform plot filters are independent of each other.

Acceleration: The vector measurement of the acceleration (rate of change of velocity) and the direction of the acceleration. Acceleration units are meters per second per second (or meters per second squared – m/s²).

Accelerometer: A seismic sensor based on a mass mounted on a piezoelectric material. The inertia of the mass when the accelerometer is moved (vibrated) results in a force on the piezoelectric material, which creates a signal. The voltage generated by the piezoelectric material is proportional to the acceleration.

Attenuate: A reduction in amplitude of a vibration over distance due to scattering and absorption (and conversion to heat). High frequencies are more easily attenuated than low ones, so close earthquake signals include both high and low frequencies, whereas distant earthquake signals only have low frequencies remaining. The typical tapering shape of an earthquake signal on a spectrogram is due to attenuation.

Color Map: A continuous progression of colors used to visualize values as color. For example, the Inferno color map used on Raspberry Shake Data View Spectrogram starts at black for zero and progressively changes through purples, reds, oranges and yellows for full scale.

Figure 21: Perceptually Uniform Sequential Colormaps

Displacement: The vector measurement of the distance and direction of movement. Displacement units are in metres (m).

FFT: Fast Fourier Transform. A mathematical algorithm to determine what pure sine and cosine wave frequencies make up a signal. Typically displayed as a graph showing the relative amplitudes of all the frequencies making up the signal.

Fourier Series: An infinitely long sum of mathematical terms involving sine and cosine waves, which is used to build waveforms mathematically. Each term specifies the amplitude and frequency of a wave in the signal, and the amplitude and frequency are related, but that relationship changes depending on the waveform being constructed. From the Fourier series for square (step) waves and spikes, we know that sudden events like earthquakes, impacts, and explosions produce all frequencies at the source. Still, due to attenuation, the higher frequencies gradually fade from the signal over distance.

Full Scale: The maximum value represented in a graph or color map.

Geophone: A seismic sensor that uses a magnet moving in a coil to generate a signal. The voltage produced is proportional to the velocity of movement (vibration).

Helicorder: A display of the seismograph signal for an extended period of time (typically 8 or 24 hours) where each line represents a smaller period (usually, 15 or 30 minutes). It simulates the original seismogram plots from drum-type seismographs where a pen plotted the earth displacement in a continuous spiral around a drum.

Longitudinal:

Means along the direction of motion of a wave. A particle subject to a longitudinal wave moves back and forth in the same direction as the wave. Sound is made of longitudinal waves.

PSD: Power Spectral Density. An extension of the FFT, a PSD shows the relative Power required by each frequency to make up the original signal.

Plate Tectonics: The theory of plates (sections of the Earth’s crust) moving on the Earth’s mantle.

Spectrogram: A plot of frequency against time, showing the relative intensities of all frequencies by virtue of color. Useful for visualizing changes in frequency as well as timing.

Spectrum: Spectrum is a general term for a plot of a function of amplitude (on the Y axis) against frequency (on the X axis). Both FFTs and PSDs are spectra (plural of spectrum). Other functions of amplitude may also be used to produce a spectrum.

Transverse: Means across or perpendicular to the direction of motion of a wave. A transverse wave results in particles moving sideways, or perpendicular, to the direction in which the wave moves. A Mexican wave in a crowd is a transverse wave. Ripples on a pond are transverse waves.

Velocity: The vector measurement of the speed and direction of movement. Velocity units ate meters per second (m/s).

Volcanism: Relating to Volcanoes.